This content is over 19 years old. It may be obsolete and may not reflect the current opinion of the author.
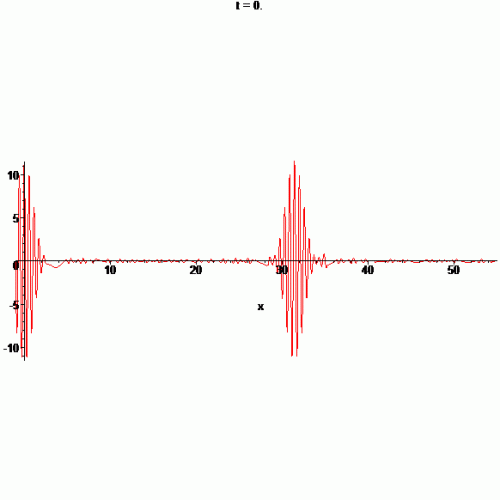
這是用Maplesoft Maple做的波包動畫Demo,要看會動的版本請按All Sizes(警告:700k GIF)。從動畫可以看出來波包以群速度向+x的方向移動,而且隨著時間能量慢慢的散開。
相對於波包在物理中的重要意義,波包的數學相當簡單;近代物理中的物質波、電磁波波速與能量傳播的速度的關係都與波包有關係。
This is an animation generated by Maplesoft Maple. See it in action in the All Sizes page (Warning: 700k GIF). You can see it travels in group velocity, and the energy decays from time to time.
這是電磁學老師找我做的動畫啦;因為沒有時間研究傅利葉積分,因此這個動畫的波包是用21個cosine波加起來的(當然是用不同的波速和震幅)。以下是我用的函數:
ƒ(x) = Σ kA(k)cos(kx-ω(k)t)
其中,
k=10, 10.2, 10.4, … , 12
A(k) = 11/(11+10(11-k)2)
ω(k) = 2*k3/2-113/2+2
如果您手邊有Maple,您可以改改我的 A(k) 和 ω(k) ,看看會不會有更漂亮的波包出現;以下是指令:
with(plots):
k0 := 11;
omega := k -> 2*k^1.5-k0^1.5+2;
A := k -> k0/(k0+(k0-k)^2*10);
animate( plot, [sum(A(k0+n/5)*cos((k0+n/5)*x-omega(k0+n/5)*t),n=-10...10),x=-1..55], t=0..5, frames=51);
I made it as requested by the teacher of EM lesson. Having no time to construct one using Fourier Integral, I simply adds 21 cosine waves (with different amplitude and velocity of course). Here are my formulae:
ƒ(x) = Σ kA(k)cos(kx-ω(k)t)
where,
k=10, 10.2, 10.4, … , 12
A(k) = 11/(11+10(11-k)2)
ω(k) = 2*k3/2-113/2+2
Try it yourself if you have Maple in hand. Change my A(k) and ω(k) to see what will happen. Here are Maple commands:
with(plots):
k0 := 11;
omega := k -> 2*k^1.5-k0^1.5+2;
A := k -> k0/(k0+(k0-k)^2*10);
animate( plot, [sum(A(k0+n/5)*cos((k0+n/5)*x-omega(k0+n/5)*t),n=-10...10),x=-1..55], t=0..5, frames=51);